Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Dessins et plans, Jeux d'extérieur, Anglais (langue), Numération, Marelles, Onze (le nombre), Marelle à cloche pied, Jeux méthématiques
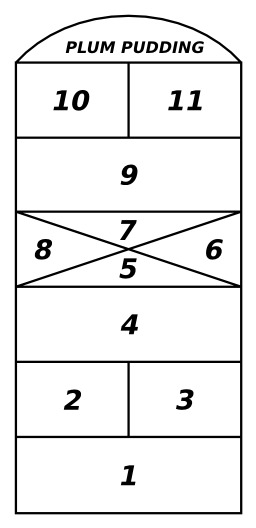
Marelle anglaise à onze cases
Marelle anglaise à onze cases et "Plum pudding" comme ciel, in D. C. Beard, "The Outdoor Handy Book: For the Playground, Field, and Forest", 1900 : "Hopscotch court", p. 356, fig. 291.
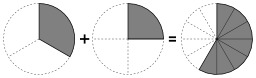
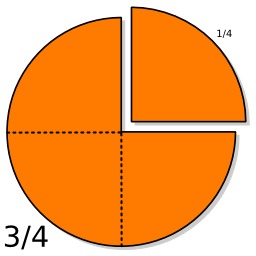
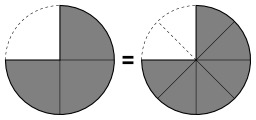
Addition de deux fractions
Addition de deux fractions matérialisées par des parts de gâteaux : 1/2 + 1/4 = 3/4.
Dessins et plans, Cartes à jouer, Jeux mathématiques, Rouge, Chiffres, Losanges, Dessin géométrique, As (cartes à jouer), Carreau (cartes à jouer), Carreaux (cartes à jouer)
As de carreau
Schéma d'un as de carreau. La carte ne présente ici aucune décoration particulière ; elle comporte deux index dans les coins supérieur gauche et inférieur droit, la valeur étant indiquée par "1".
Dessins et plans, Cartes à jouer, Jeux mathématiques, Rouge, Losanges, Dessin géométrique, As (cartes à jouer), Carreaux (cartes à jouer)
As de carreau
L'as de carreau a pour valeur l'as et pour enseigne le carreau. En abrégé, il est noté "1♦", plus rarement "A♦" comme ici. De façon générale, l'as de carreau peut être la plus forte carte des carreaux, suivant immédiatement le roi de carreau, ou la plus petite, précédant le deux de carreau. L'élément principal de la carte est un losange, situé en son centre, indiquant à la fois sa valeur et son enseigne. Source : http://fr.wikipedia.org/wiki/As_de_carreau
Dessins et plans, Cartes à jouer, Jeux mathématiques, Rouge, Coeur, Nombres, Chiffres, As (cartes à jouer)
As de coeur
Schéma d'un as de cœur. La carte ne présente ici aucune décoration particulière ; elle comporte deux index dans les coins supérieur gauche et inférieur droit, la valeur étant indiquée par "1".
As de coeur
Schéma d'un as de cœur. La carte ne présente ici aucune décoration particulière ; elle comporte deux index dans les coins supérieur gauche et inférieur droit, la valeur étant indiquée par "A".
Dessins et plans, Cartes à jouer, noir, Jeux mathématiques, As (cartes à jouer), Trèfles (cartes à jouer)
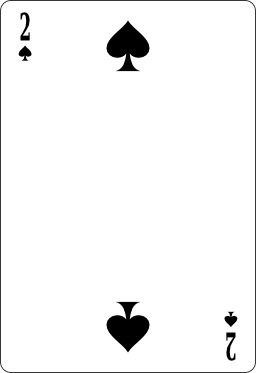
As de trèfle
Schéma d'un as de trèfle. La carte ne présente ici aucune décoration particulière ; elle comporte deux index dans les coins supérieur gauche et inférieur droit, la valeur étant indiquée par "1" au lieu d'un "A". L'as de trèfle a pour valeur l'as et pour enseigne le trèfle. En abrégé, il est noté "1♣", plus rarement "A♣". Source : http://fr.wikipedia.org/wiki/As_de_tr%C3%A8fle L'as de trèfle fait partie des jeux de cartes occidentaux traditionnels. En particulier, on la retrouve dans les jeux de 32 cartes, de 52 cartes et de tarot. De façon générale, l'as de trèfle peut être la plus forte carte des trèfles, suivant immédiatement le roi de trèfle, ou la plus petite, précédant le deux de trèfle.
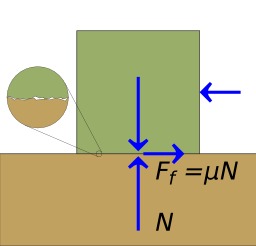
Coefficient de frottement
Coefficient de frottement : Le frottement vec{F} s'oppose au mouvement relatif entre les deux corps. Le frottement statique est une force qui tend à garder un corps en état statique. Elle dépend du poids apparent du corps et du coefficient de frottement statique, évalué en fonction de la nature des surfaces en contact. Lorsqu'une force est appliquée sur un objet au repos, la composante parallèle à la surface de la force est compensée par la force de frottement statique jusqu'à la valeur maximale de cette dernière. Mathématiquement, le frottement statique f_s est plus petit ou égal au coefficient de frottement statique mu_s multiplié par le poids apparent N.
Dessins et plans, Communication, Linguistique, Analyse de contenu (communication), Communication et technologie, Communications militaires, Communication téléphonique, Compétence de communication (linguistique), Messages chiffrés, Transmissions
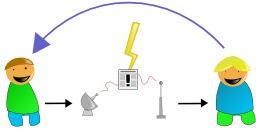
Communication linéaire
Le modèle de Claude Shannon et Weaver désigne un modèle linéaire simple de la communication : cette dernière y est réduite à sa plus simple expression, la transmission d'un message. On peut résumer ce modèle en : Un émetteur, grâce à un codage, envoie un message à un récepteur qui effectue le décodage dans un contexte perturbé de bruit. Apparu dans "Théorie mathématique de la communication" (1948), ce schéma sert à deux mathématiciens Claude Shannon (père entre autres de nombreux concepts informatiques modernes) et Warren Weaver (scientifique versé tant dans la vulgarisation que la direction de grands instituts), à illustrer le travail de mesure de l'information entrepris pendant la Seconde Guerre mondiale par Claude Shannon (ce dernier a été embauché par Weaver à l'Office of Scientific Research and Development pour découvrir, dans le code ennemi, les parties chiffrées du signal au milieu du brouillage). À l'origine, les recherches de Shannon ne concernent pas la communication, mais bien le renseignement militaire. C'est Weaver qui a "traduit" la notion de brouillage par celle de "bruit", la notion de signal par "message", la notion de codeur par "émetteur", la notion de décodeur par "récepteur". Jusqu'à la fin de sa vie, Claude Shannon se défendra contre la reprise du soi-disant modèle pour autre chose que des considérations mathématiques. Le modèle dit de Shannon et Weaver n'a en effet de prétention qu'illustrative. Mais il a souvent été pris au pied de la lettre, révélant alors la forte influence béhavioriste du modèle de Pavlov (stimulus-réponse).
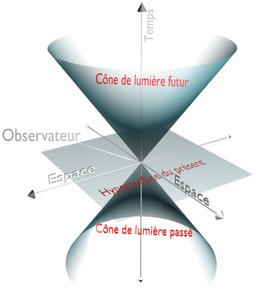
Cône de lumière
Représentation schématique de l'espace de Minkowski, qui montre seulement deux des trois dimensions spatiales : cône de lumière. Un espace de Minkowski, du nom de son inventeur Hermann Minkowski, est un espace affine mathématique à quatre dimensions modélisant l'espace-temps de la relativité restreinte : les propriétés physiques présentes dans cette théorie correspondent à des propriétés géométriques de cet espace, la réciproque n'étant pas vraie car le réalisme physique n'est pas entièrement contenu dans cette géométrisation.
Courbure de l'espace-temps sous le poids de la Terre
Illustration de l'influence d'une masse (ici, la Terre) sur l'espace-temps. En physique, l'espace-temps est une représentation mathématique de l'espace et du temps comme deux notions inséparables et s'influençant l'une l'autre, suite à l'apparition de la relativité restreinte et sa représentation géométrique qu'est l'espace de Minkowski, et dont l'importance a été renforcée par la relativité générale. Cette conception de l'espace et du temps est l'un des grands bouleversements survenus au début du XXe siècle dans le domaine de la physique, mais aussi pour la philosophie.
Dessins et plans, animaux prédateurs, Populations, Probabilités, Prédateurs et proies, Biologie des populations, Équations, Équations d'évolution, Équations différentielles
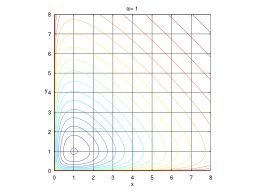
Équations proie-prédateur de Lotka-Volterra
Courbes d'évolution d'un système complexe, formé de deux espèces, proie et prédateur : équations de Lotka-Volterra. L'effectif des proies est x(t), celui des prédateurs y(t) . On retombe sur le cas précédent si y est nul. La quantité x(t)y(t) est une probabilité de rencontre, qui influe négativement sur une population (les proies), positivement sur l'autre (les prédateurs). À chaque instant, connaissant les populations en présence, on peut décrire la tendance. Ces deux équations sont couplées c'est-à-dire qu'il faut les résoudre ensemble. Mathématiquement, il faut les concevoir comme une seule équation d'inconnue le couple (x(t),y(t)) . Si l'effectif initial des populations est connu, l'évolution ultérieure est parfaitement déterminée. Elle se fait le long d'une des courbes d'évolution figurées ci-contre, qui laissent apparaître un comportement cyclique.
Dessins et plans, Géométrie, Triangle, Mathématiciens, Itération (mathématiques), Algorithmes, Savants polonais, Wacław Sierpinski (1882-1969), Fractales, Récursivité, Théorie de la
Évolution du triangle de Sierpinski
Évolution du triangle de Wacław Sierpinski (1882-1969) en 5 itérations. Un algorithme pour obtenir des approximations arbitrairement proches du triangle de Sierpiński peut s'écrire de la manière suivante : 1-Commencer à partir d'un triangle quelconque du plan. Le triangle canonique de Sierpiński se construit à partir d'un triangle équilatéral ayant une base parallèle à l'axe des abscisses ; 2-Tracer les trois segments qui joignent deux à deux les milieux des côtés du triangle, ce qui délimite 4 nouveaux triangles ; 3-Enlever le petit triangle central. Il y a maintenant trois petits triangles qui se touchent deux à deux par un sommet, dont les longueurs des côtés sont la moitié de celles du triangle de départ (obtenue par une homothétie de rapport 1/2), et dont l'aire est divisée par 4. 4-Recommencer à la deuxième étape avec chacun des petits triangles obtenus.
Photographie, Jeux mathématiques, Diamants, Jeux de ficelles, Jeux de ficelle, Osage (Indiens) -- Art, Osages (Indiens)
Figure du jeu de ficelle des deux diamants
Jeu indien Osage de ficelle des deux diamants : double noeud. Source : Caroline Furness Jayne, String Figures and How to Make Them, 1962, page 30.
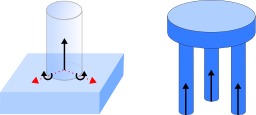
Force appliquée selon un appui plan
Force appliquée selon un appui plan : la liaison appui plan, appelée aussi liaison plane, présente 3 degrés de liaison. Ils forcent le mouvement à rester dans un plan. Les deux translations et la rotation dans ce plan sont libres. L'appui des trois pieds d’un tabouret sur un sol plan constitue une liaison plane. Le quatrième pied d’une chaise ne touche le sol que si les extrémités des pieds sont parfaitement coplanaires ; le système est alors hyperstatique les liaisons étant en surnombre par rapport au besoin de guidage. Un mécanisme est l'association de plusieurs pièces liées entre elles par des contacts physiques qui les rendent totalement ou partiellement solidaires, selon qu'ils autorisent ou non des mouvements relatifs. La liaison mécanique est le modèle utilisé pour décrire cette relation dont la considération est primordiale dans l'étude des mécanismes. Elle emploie des représentations mathématiques qui diffèrent suivant qu'on l'aborde sous l'aspect cinématique (étude des mouvements ou guidages) ou sous l'aspect statique (étude de la transmission d'efforts). La notion de liaison mécanique se définit plus généralement entre groupes de pièces, appelés classes d'équivalence contenant respectivement des pièces entièrement solidaires. Un mécanisme est l'association de plusieurs pièces liées entre elles par des contacts physiques qui les rendent totalement ou partiellement solidaires, selon qu'ils autorisent ou non des mouvements relatifs. Elle emploie des représentations mathématiques qui diffèrent suivant qu'on l'aborde sous l'aspect cinématique (étude des mouvements ou guidages) ou sous l'aspect statique (étude de la transmission d'efforts). La notion de liaison mécanique se définit plus généralement entre groupes de pièces, appelés classes d'équivalence contenant respectivement des pièces entièrement solidaires.
Hexagone magique (3)
Hexagone magique d'ordre 3 : les nombres de 1 à 19 sont placés dans cette grille hexagonale de manière à ce que la somme des nombres de chaque rangée soit égale à 38. En mathématiques, un hexagone magique d'ordre n est un arrangement de nombres formant un gabarit hexagonal centré avec n cellules sur chaque côté. La somme des nombres dans chaque rangée ou dans les trois directions font la même somme. Un hexagone magique normal contient tous les entiers allant de 1 à 3n2 − 3n + 1. Il existe seulement deux arrangements respectant ces conditions, celui d'ordre 1 et celui d'ordre 3. De plus, la solution d'ordre 3 est unique.
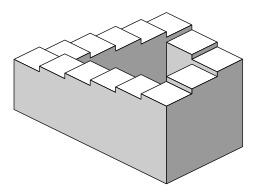
L'escalier impossible de Penrose
Illusion d'optique de l'escalier impossible de Penrose conçu en 1958 par le généticien britannique Lionel Penrose, en se basant sur le triangle de Penrose créé par son fils, le mathématicien Roger Penrose. Il illustre un problème de topologie mathématique. L'escalier de Penrose est une représentation en deux dimensions d'un escalier faisant quatre virages à angle droit, revenant ainsi à son point de départ ; en principe, il devrait y avoir une différence de niveau entre les deux extrémités, mais les perspectives de la représentation sont distordues de sorte qu'au contraire, elles paraissent se rejoindre. De cette manière, la figure donne l'impression que les marches forment une boucle, constituant une perpétuelle montée (ou descente, selon le sens de rotation) ; en d'autres termes, il semble n'y avoir ni point le plus haut, ni point le plus bas. Source : https://fr.wikipedia.org/wiki/Escalier_de_Penrose
Dessins et plans, Arithmétique, Treizième siècle, Blaise Pascal (1623-1662), Mathématiques, Lapins, Triangle de Pascal, Populations d'animaux, Suite de Fibonacci
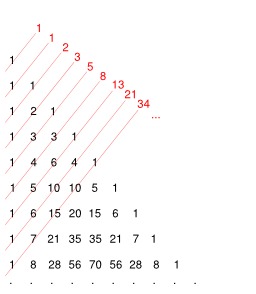
La suite de Fibonacci
Triangle de Pascal et suite de Fibonacci : La somme des diagonales ascendantes du triangle de Pascal forme la suite de Fibonacci. Leonardo Fibonacci (v. 1175-1250). Elle doit son nom à Leonardo Fibonacci, dit Leonardo Pisano, un mathématicien italien du XIIIe siècle qui, dans un problème récréatif posé dans un de ses ouvrages, le Liber Abaci, décrit la croissance d'une population de lapins : « Un homme met un couple de lapins dans un lieu isolé de tous les côtés par un mur. Combien de couples obtient-on en un an si chaque couple engendre tous les mois un nouveau couple à compter du troisième mois de son existence ? » Cette suite est fortement liée au nombre d'or, φ (phi). Ce nombre intervient dans l'expression du terme général de la suite. Inversement, la suite de Fibonacci intervient dans l'écriture des réduites de l'expression de φ (phi) en fraction continue : les quotients de deux termes consécutifs de la suite de Fibonacci sont les meilleures approximations du nombre d'or.
Le jeu de Pentago
Le jeu de pentago est un jeu de stratégie abstrait pour deux joueurs inventé par la compagnie suédoise Mindtwister. Le jeu est joué sur un tablier 6x6, divisé en quatre tabliers secondaires 3x3. À chaque tour, chaque joueur place une bille de sa couleur (noire ou blanc) sur un espace inoccupé sur le tablier, et puis tourne un des tabliers secondaires de 90 degrés dans le sens des aiguilles d'une montre ou dans le sens contraire. Un joueur gagne en obtenant cinq de ses billes dans une rangée verticale, horizontale ou diagonale (avant ou après la rotation du tablier). Si chacun des 36 espaces est occupé sans que ne soit formé une rangée de cinq billes de la même couleur, alors la partie est nulle.
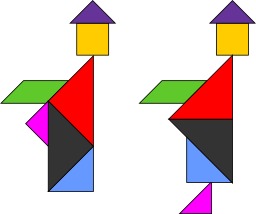
Le tangram des deux moines
Tangram du paradoxe des deux moines : même nombre de pièces mais disposées différemment.
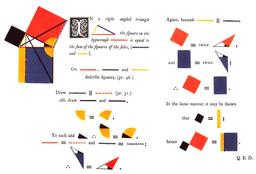
Le théorème de Pythagore
Démonstration du théorème : dans un triangle rectangle, le carré de l'hypothénuse est égal à la somme des carrés des deux côtés.
Textes, Dix-septième siècle, Latin (langue), Isaac Newton (1642-1727), Principes mathématiques de la philosophie naturelle - Isaac Newton (1642-1727), Savants anglais
Les lois de Newton en latin
"AXIOMATA SIVE LEGES MOTUS" d'Isaac Newton, édition de 1687. Les deux premières lois de Newton en latin dans l'édition originale du "Principia Mathematica" de 1687.
Photographie, Vie en banlieue, Jeux mathématiques, Jeux d'extérieur, Rues, Craie, Banlieues, Numération, Nu-pieds (sandales), Sandales, Marelles, Jeux de plein air, Art dans la rue, Photographie de rue, Marelle à cloche pied
Marelle interminable dans la rue
Marelle interminable dans la rue dessinée à la craie par deux enfants pieds-nus.
Dessins et plans, Musique, Mathématiques, Notes (musique), Espaces harmoniques, Harmoniques (musique)
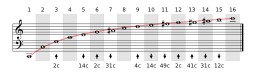
Mathématiques et musique
Cette image indique les harmoniques du do1 sur une portée, et précisent par les flèches et les chiffres (en cents) l’écart de hauteur entre chacun des 16 premiers harmoniques et la note la plus proche dans la gamme tempérée. Considérant que le demi-ton (du tempérament égal) fait 100 cents, la déviation de 49 cents de l'harmonique 11 est donc quasiment à mi-chemin entre deux notes existantes, c’est-à-dire un quart de ton.
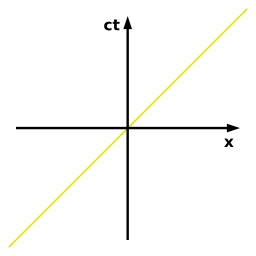
Minkowski, le trajet d'un photon
Référentiel inertiel de Minkowski : Ligne d'univers du photon. En jaune le trajet d'un photon x = ct, avec c = vitesse de la lumière. Le diagramme de Minkowski est un diagramme d'espace-temps développé en 1908 par Hermann Minkowski, qui fournit une représentation des propriétés de l'espace-temps défini par la théorie de la relativité restreinte. Il permet une compréhension qualitative et intuitive de phénomènes comme la dilatation du temps, la contraction des longueurs ou encore la notion de simultanéité, sans utiliser d'équations mathématiques. Pour la lisibilité du diagramme, une seule dimension spatiale est représentée. Contrairement aux diagrammes distance/temps usuels, la coordonnée spatiale est en abscisse et le temps en ordonnée. Les objets décrits par ce diagramme peuvent être pensés comme se déplaçant du bas vers le haut à mesure que le temps passe. La trajectoire d'un objet dans ce diagramme est appelée ligne d'univers. Une particule immobile aura une ligne d'univers verticale. Chaque point du diagramme représente une certaine position dans l'espace et le temps. Cette position est appelée un événement, indépendamment du fait qu'il se passe réellement quelque chose en ce point ou non. Pour faciliter l'utilisation du diagramme, l'axe des ordonnées représente une quantité "ct" qui est le temps multiplié par la vitesse de la lumière "c". Cette quantité est assimilable également à une distance. De cette manière, la ligne d'univers du photon est une droite de pente 45°, l'échelle des deux axes étant identique dans un diagramme de Minkowski.
Dessins et plans, Géométrie, Jeux mathématiques, Rubans, Ruban adhésif, Mathématiques récréatives, Ferdinand Möbius (1790-1868), Collages (art)
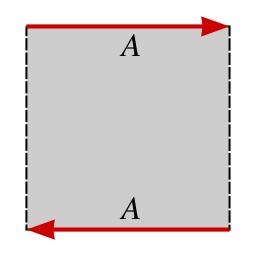
Montage d'un ruban de Möbius
Schéma de montage d'un ruban de Möbius : recoller les deux flèches en respectant le sens.
Dessins et plans, Jeux mathématiques, Jeux de logique, Grilles, Influence japonaise, Kakuro, Mots-croisés
Mots-croisés japonais
Grille de Kakuro avec solution, jeu de mots-croisés japonais. Outre la ligne du haut et la colonne de gauche, entièrement noires, la grille, telle une grille de mots-croisés, est divisée en « mots » horizontaux ou verticaux par les cases noires. Les cases noires elles-mêmes sont divisées en deux par une diagonale allant du coin en haut à gauche au coin en bas à droite, de sorte que le "mot" à sa droite et le "mot" au-dessous puissent être définis dans la même case. L'objectif du jeu est de remplir les cases vides (blanches) avec des chiffres entre 1 et 9 de sorte que la somme de tous les chiffres d'un nombre soit égale au nombre inscrit dans la case remplie (noire) définissant le nombre, et qu'un nombre ne puisse pas contenir deux fois le même chiffre. Cette dernière règle est celle qui rend possible la création de grilles à solution unique. Source : http://fr.wikipedia.org/wiki/Kakuro.
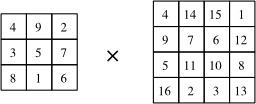
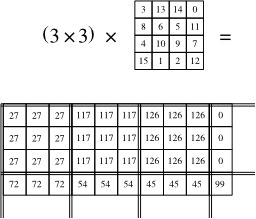
Multiplication de deux carrés magiques - 1
Multiplication de deux carrés magiques : Soit à effectuer le « produit » de ces deux carrés magiques, un de 3x3 et l'autre de 4x4. Le carré magique final sera de 12x12. Le « produit » de deux carrés magiques crée un carré magique d'ordre supérieur aux deux multiplicandes. Ce produit s'effectue ainsi. Soit les carrés magiques M et N : 1) Le carré final sera d'ordre MxN ; 2) Diviser le damier final en NxN sous-damiers de MxM cases ; 3) Dans le carré N, réduire de 1 la valeur de tous les nombres ; 4) Multiplier ces valeurs réduites par M × M. Les résultats sont reportés dans les cases de chaque sous-damier correspondant du carré final ; 5) Les cases du carré M sont additionnées NxN fois aux cases du damier final. Source : http://fr.wikipedia.org/wiki/Carr%C3%A9_magique_%28math%C3%A9matiques%29.
Dessins et plans, Calcul, Jeux mathématiques, Multiplication (arithmétique), Carrés magiques, Démonstration (logique)
Multiplication de deux carrés magiques - 2
Deuxième étape de la multiplication des deux carrés magiques (3 et 4) : Le carré magique de 3x3 est remplacé par le produit (3 × 3), alors que chaque nombre du carré 4x4 est diminué de 1. Le damier final, de taille 12x12, est divisé en 4x4 sous-damiers, chacun ayant 3x3 cases. Chacune de ses cases s'obtient en multipliant (3 × 3) par l'une des cases du carré magique 4x4 « diminué ». Par exemple, 117 est le produit de 3 × 3 × 13. Ce carré est magique, mais n'est pas normal. La prochaine étape va « corriger » cette « anomalie ».
Dessins et plans, Calcul, Jeux mathématiques, Multiplication (arithmétique), Carrés magiques, Démonstration (logique)
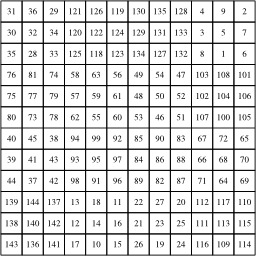
Multiplication de deux carrés magiques - 3
Multiplication de deux carrés magiques, dernière étape : Après 4x4 additions du carré 3x3, le carré final est magique et normal.
Dessins et plans, Bleu, Rouge, Jaune, Cercles, Mathématiques, Trois (le nombre), Entrelacs (arts décoratifs), Théorie des noeuds, Anneaux topologiques
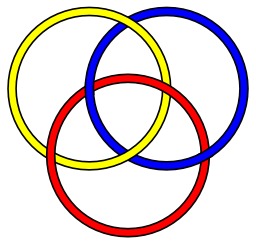
Noeud borroméen en couleur
Nœud borroméen standard. Deux quelconques des cercles sont posés l'un sur l'autre sans se croiser et pourtant l'ensemble des trois cercles est lié par l'un d'entre eux.
Dessins et plans, Cercles, Mathématiques, Trois (le nombre), Entrelacs (arts décoratifs), Théorie des noeuds, Anneaux topologiques
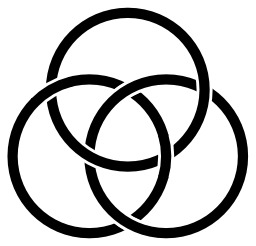
Noeud borroméen en noir et blanc
Nœud borroméen standard. Deux quelconques des cercles sont posés l'un sur l'autre sans se croiser et pourtant l'ensemble des trois cercles est lié par l'un d'entre eux.
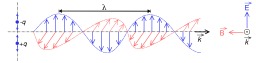
Onde électromagnétique
Onde électromagnétique : oscillation couplée du champ électrique et du champ magnétique, modèle du dipôle vibrant. Le vecteur \vec{k} indique la direction de propagation de l'onde. On ne peut en fait voir le photon que comme une particule quantique, c’est-à-dire un objet mathématique défini par sa fonction d’onde qui donne la probabilité de présence. Attention à ne pas confondre cette fonction et l’onde électromagnétique classique. Ainsi, l’onde électromagnétique, c’est-à-dire la valeur du champ électrique et du champ magnétique en fonction de l’endroit et du moment (\vec{E}(\vec{x},t) et \vec{B}(\vec{x},t)), a donc deux significations. Fonction macroscopique : lorsque le flux d’énergie est suffisamment important, ce sont les champs électrique et magnétique mesurés par un appareil macroscopique (par exemple antenne réceptrice, un électroscope ou une sonde de Hall) ; Fonction microscopique : elle représente la probabilité de présence des photons, c’est-à-dire la probabilité qu’en un endroit donné il y ait une interaction quantifiée (c’est-à-dire d’une énergie hν déterminée).
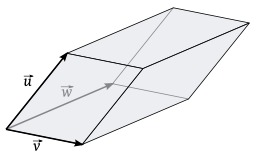
Parallélépipède déterminé par trois vecteurs
Parallélépipède déterminé par trois vecteurs. En géométrie dans l'espace, les parallélépipèdes sont des hexaèdres dont les faces sont parallèles deux à deux.
Pavage d'hexagones et de triangles
Pavage régulier à partir de deux formes géométriques, un hexagone (jaune) et un triangle (bleu).
Dessins et plans, Géométrie, Jeux mathématiques, Pavages (mathématiques), Mathématiciens, Tuiles, Divertissements mathématiques
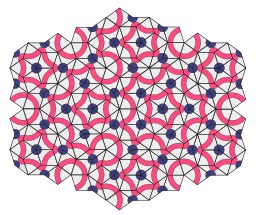
Pavage de Penrose avec tuiles apériodiques
Pavage de Penrose réalisé avec deux tuiles apériodiques. Roger Penrose est un mathématicien anglais. Les pavages de Penrose présentent une symétrie d'ordre 5 (invariance par rotation d'angle 2π/5 radian, soit 72 degrés). Ils ne sont pas périodiques, c'est-à-dire qu'on ne peut les décrire comme un motif répété sur une grille régulière. Ils sont cependant quasi-périodiques, c'est-à-dire que tout motif apparaissant dans le pavage réapparaît régulièrement. Plus généralement toute portion finie du pavage, aussi grande soit-elle, se répète infiniment dans le pavage. Les pavages de Penrose ne seraient restés qu'un joli divertissement mathématique si n'avaient été découverts, en 1984, des matériaux présentant une structure fortement ordonnée comme celle des cristaux mais non périodique : les quasi-cristaux. Les pavages non périodiques, en particulier ceux de Penrose, s'avérèrent alors un modèle plausible de ces étranges matériaux. Cette découverte illustra à nouveau ce que Roger Penrose lui-même avait déjà remarqué en 1973, à propos d’un sujet de relativité générale : « On ne sait jamais vraiment quand on perd son temps ». Source : http://fr.wikipedia.org/wiki/Pavage_de_Penrose.
Pavage jaune, bleu et vert
Pavage régulier obtenu avec deux formes géométriques, un carré (jaune) et un triangle (bleu, vert).
Dessins et plans, Pommes, Numération, Trois (le nombre), Deux (le nombre), Outils pédagogiques, Un (le nombre), Nombres entiers naturels
Pyramide de six pommes
Pyramide de six pommes : Les entiers naturels permettent de compter (une pomme, deux pommes, trois pommes…). En mathématiques, un entier naturel est un nombre positif (pouvant donc être nul) permettant fondamentalement de dénombrer des objets comptant chacun pour un. Un tel nombre entier peut s'écrire avec une suite finie de chiffres en notation décimale positionnelle (sans signe et sans virgule). Source : http://fr.wikipedia.org/wiki/Entier_naturel Les entiers naturels sont donc, outre zéro, ceux que l'on commence à énumérer avec la comptine numérique : un, deux, trois, quatre…
Photographie, Géométrie, Jeux mathématiques, Rubans, Ruban adhésif, Pliages en papier, Mathématiques récréatives, Ferdinand Möbius (1790-1868)
Ruban de Moebius
Ruban de Moebius construit à partir d'une bande de papier, un ruban adhésif retenant les deux bouts. Il est facile de visualiser la bande de Möbius dans l'espace : un modèle simple se réalise en faisant subir une torsion d'un demi-tour à une longue bande de papier, puis en collant les deux extrémités. En topologie, le ruban de Möbius (aussi appelé bande de Möbius ou boucle de Möbius) est une surface compacte dont le bord est homéomorphe à un cercle. Autrement dit, il ne possède qu'une seule face contrairement à un ruban classique qui en possède deux. Elle a la particularité d'être réglée et non-orientable. Source : http://fr.wikipedia.org/wiki/Ruban_de_M%C3%B6bius.
Synthèse additive des couleurs
Représentation de la synthèse additive des couleurs : En 1931, la commission internationale de l'éclairage (CIE) a fixé des primaires mathématiques de référence pour les calculs, en adoptant les longueurs d'onde suivantes : 1) rouge : chiffre rond de 700 nm, 2) vert : 546,1 nm (correspondant à une raie spectrale du mercure), 3) bleu : 435,8 nm (autre raie du mercure). Les couleurs secondaires obtenues par addition de deux couleurs primaires sont le magenta (R+B), le jaune (R+V) et le cyan (B+V). La somme des trois flux donne de la lumière blanche (R+B+V). La modulation de l'intensité des flux lumineux additionnés permet d'obtenir toutes les teintes intermédiaires. Source : wikipedia, Couleur_primaire.